A Bond-Based Machine Learning Model for Molecular Polarizabilities and A Priori Raman Spectra
Why I chose this paper
- Reconstructing IR/Raman spectra is interesting to me
- Applications of ML to electronic structure theory (outside of potential) is cool
Introduction
- Machine learning force fields (ML FF) have accelerated the field of molecular simulations – specifically for systems where there is not an established force field
- ML FFs are significantly more cost-efficient
- Learning molecular properties like dipole moment (IR) and polarizability (Raman) can help in interpreting spectra signals and benchmarking ML accuracy against experiment
- Neural network algorithms v.s. kernel algorithms
- NN: better performance + lower cost for larger systems
- kernel: requires less data + high cost for large systems
Existing Work on ML Models for Electric Polarizability
- Equivariant neural networks, response formalism, Applequists’s dipole interaction model
- Two kernel-based methods
- align structures in training data and treat tensor components as scalars
- requires lots of data
- symmetry-adapted Gaussian regression
- generalization of scalar kernel ridge regression (KRR)
- align structures in training data and treat tensor components as scalars
Goal of this work
- KRR on bond polarizability model (BPM)
- molecular polarizability is a sum over bond contributions
Theory
Bond Polarizability Model
- total molecular polarizability, \(\alpha\) is the sum of bond polarizabilities
\[ \alpha = \sum_b{\alpha^b} \]
- elements of individual bond polarizability tensors
\[ \alpha_{ij}^{b} = \frac{1}{3}(2\alpha_p^b + \alpha_l^b)\delta_{ij} + (\alpha_l^b + \alpha_p^b)(\hat{R}_i^b\hat{R}_j^b - \frac{1}{3}\delta_{ij}) \]
- assumes bonds are cylindrically symmetric and typically assumes total polarizability only depends on bond length
ML Model
- Separate polarizability tensor into isotropic and anisotropic components so the ML task is to infer these
\[ \alpha = \alpha_{\text{iso}}\bf{1}+\beta \]
- Rewrite elements of tensor in terms of components
\[ \alpha_{ij}^{b} = \alpha_{\text{iso}}^b\delta_{ij} + \beta^b(\hat{R}_i^b\hat{R}_j^b - \frac{1}{3}\delta_{ij}) \]
- KRR used to evaluate isotropic component, summed over bonds instead of atoms
\[ \alpha_{\text{iso}} = \sum_b{\alpha_{\text{iso}}^b} = \sum_n{\sum{K(\textbf{q}^b},\textbf{q}^{b'})w_n} \]
- Using a Gaussian kernel
\[ K(\textbf{q}^b,\textbf{q}^{b'}) = \text{exp}(-\gamma||\textbf{q}^b-\textbf{q}^{b'}||^2) \]
- The same can be done for anisotropic component
\[ \beta_{ij} = \sum_b{\beta^bQ_{ij}^b} = \sum_n{\sum_{b,b'}{K(\textbf{q}^b},\textbf{q}^{b'})Q_{ij}^bv_n} \]
- loss function
\[ \mathcal{L} = \frac{1}{2}\sum_{i,j}{||\beta_{ij} - \textbf{K}_{ij}\textbf{v}||^2} \]
Raman Spectra
- Calculating the anharmonic IR and Raman spectra
\[ I_{\text{iso}}(\omega) \propto v(\omega) \int{dt \ e^{i\omega t}\langle\dot{\alpha}_{\text{iso}}(\tau)\dot{\alpha}_{\text{iso}}(t-\tau)}\rangle_\tau \] \[ I_{\text{aniso}}(\omega) \propto v(\omega) \int{dt \ e^{i\omega t}\langle Tr[\dot{\beta}_{\text{iso}}(\tau)\dot{\beta}_{\text{iso}}(t-\tau)}]\rangle_\tau \]
Biphenyl
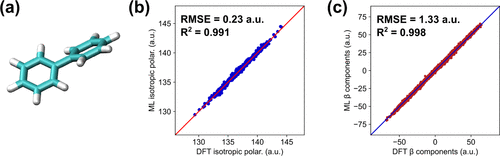
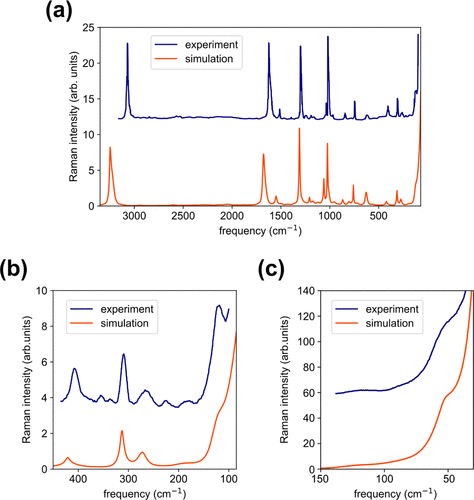
Raman spectra evaluation
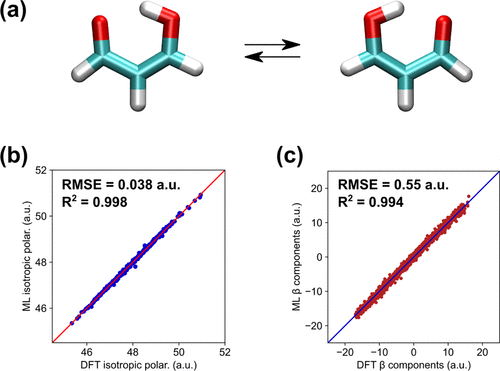
Malonaldehyde
- keto and enol forms
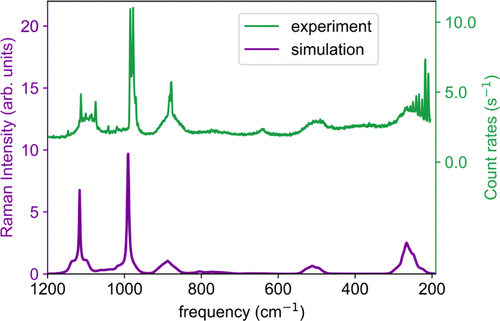
Future Directions
- Deep neural network implementation of BPM
- Consider all bonds within a cutoff region